
สำหรับเพื่อน ๆ ที่เรียนเรื่องความน่าจะเป็นกันมาแล้ว คงรู้ดีว่าเรื่องนี้สำคัญแค่ไหน นอกจากคุณครูจะออกข้อสอบที่โรงเรียนแล้ว เพื่อน ๆ ยังมีโอกาสเจอความน่าจะเป็นในข้อสอบ O-NET คณิตศาสตร์ด้วยนะ เพราะฉะนั้น ลองฝึกมือกันหน่อย กับข้อสอบที่เราคัดมาพิเศษ 7 ข้อด้านล่าง ไปทำกันเลย
1. ตารางแสดงจำนวนลูกปิงปองสีส้มและจำนวนลูกปิงปองทั้งหมดในถุงห้าใบ
| ถุงใบที่ | จำนวนลูกปิงปองสีส้ม (ลูก) | จำนวนลูกปิงปองทั้งหมด (ลูก) |
| 1 | 50 | 75 |
| 2 | 55 | 66 |
| 3 | 60 | 80 |
| 4 | 66 | 77 |
| 5 | 80 | 100 |
การสุ่มหยิบลูกปิงปอง 1 ลูกจากถุงใบใด มีโอกาสได้ลูกปิงปองสีส้มมากที่สุด
- ถุงใบที่ 1
- ถุงใบที่ 2
- ถุงใบที่ 3
- ถุงใบที่ 4
- ถุงใบที่ 5
เฉลย
ความน่าจะเป็นที่จะหยิบได้ลูกปิงปองสีส้ม = จำนวนลูกปิงปองสีส้มในถุง ⁄ จำนวนลูกปิงปองทั้งหมดในถุง
ถุงที่ 1: = ⁵⁰⁄₇₅ = ⅔
ถุงที่ 2: = ⁵⁵⁄₆₆ = ⅚
ถุงที่ 3: = ⁶⁰⁄₈₀ = ¾
ถุงที่ 4: = ⁶⁶⁄₇₇ = ⁶⁄₇
ถุงที่ 5: = ⁸⁰⁄₁₀₀ = ⅘
⅔ > ¾ > ⅘ > ⅚ > ⁶⁄₇
ดังนั้น ถุงที่ 4 มีโอกาสเยอะที่สุด
ตอบ ข้อ 4.
----------------------------------------------------------------------------------
2. กล่องใบหนึ่งมีสลากอยู่ 5 ใบ คือ สลากหมายเลข 1, 2, 3, 4 และ 5 ถ้าสุ่มหยิบสลากจากกล่องนี้ขึ้นมาสองใบพร้อมกัน เหตุการณ์ในข้อใดมีโอกาสเกิดขึ้นได้น้อยที่สุด
- ได้สลากหมายเลขคี่ทั้งสองใบ
- ได้สลากที่มีหมายเลขต่างกันอยู่ 3
- ได้สลากที่มีหมายเลขน้อยกว่า 4 ทั้งสองใบ
- ได้สลากที่มีผลรวมของหมายเลขมากกว่า 5
- ได้สลากที่มีผลรวมของหมายเลขเป็นจำนวนเฉพาะ
เฉลย
1. เลือกหมายเลขคี่ 2 ใบ จาก 3 ใบ (1, 3, 5)

2. 14, 25 = 2 วิธี
3. เลือก 2 ใบ จาก 3 ใบ (1, 2, 3) = ³ⁱ⁄₂ᵢ = 3
4. จำนวนวิธีที่ผลรวมมากกว่า 5 = จำนวนวิธีทั้งหมด - ผลบวกน้อยกว่าหรือเท่ากับ 5

Note: 4 = (12, 13, 14, 23)
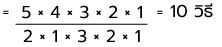
จำนวนเฉพาะที่เป็นไปได้ = 2, 3, 5, 7
โอกาสที่จะหยิบฉลากได้ผลรวมเป็น 2 = 0
โอกาสที่จะหยิบฉลากได้ผลรวมเป็น 3 = (12)
โอกาสที่จะหยิบฉลากได้ผลรวมเป็น 4=(14, 23)
โอกาสที่จะหยิบฉลากได้ผลรวมเป็น (25, 34)
ดังนั้นจำนวนวิธีที่เป็นไปได้ทั้งหมด = 5 วิธี
ตอบ ข้อ 2.
----------------------------------------------------------------------------------
3. คุณครูจับสลากรายชื่อนักเรียน 4 คน ได้แก่ กล้วย ชมพู่ ส้ม และองุ่น เพื่อจัดลำดับการนำเสนอผลงาน ถ้าคุณครูสุ่มหยิบสลากครั้งละ 1 ใบ โดยไม่ใส่คืนจนครบทั้ง 4 ใบ แล้วเหตุการณ์ที่ได้สลากที่มีชื่อส้มจากการหยิบครั้งที่หนึ่ง มีสมาชิกอยู่ทั้งหมดกี่ตัว (ข้อสอบอัตนัย)
เฉลย
ใบที่ 1 หยิบได้ส้ม เลือกได้ 1 วิธี
ใบที่ 2 หยิบใครก็ได้ 3 คนที่เหลือ เลือกได้ 3 วิธี
ใบที่ 3 หยิบใครก็ได้ 2 คนที่เหลือ เลือกได้ 2 วิธี
ใบที่ 4 หยิบใครก็ได้ 1 คนที่เหลือ เลือกได้ 1 วิธี
ดังนั้น เหตุการณ์ที่ได้สลากชื่อส้มในครั้งที่หนึ่งเท่ากับ 1 × 3 × 2 × 1 = 6 แบบ
ตอบ 6
----------------------------------------------------------------------------------
4. โรงเรียน 3 โรง ส่งตัวแทนนักเรียนมาโรงเรียนละ 2 คน เป็นชาย 1 คน หญิง 1 คน ในจำนวนตัวแทนนักเรียน 6 คนนี้ ถ้าสุ่มนักเรียน 1 คนเพื่อถือพาน และสุ่มนักเรียนอีก 1 คน จากนักเรียนที่เหลือเพื่อร้องเพลง แล้วความน่าจะเป็นที่จะได้นักเรียน 2 คนนี้เป็นเพศเดียวกันเท่ากับเท่าใด
- ⅕
- ⅓
- ⅖
- ½
- ⅔
เฉลย
เลือกจากใครก็ได้จากทั้งหมด 6 คน ได้
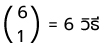

ตอบ ข้อ 3.
----------------------------------------------------------------------------------
5. สลาก 25 ใบ มีหมายเลข 1 ถึง 25 กำกับใบละ 1 หมายเลขโดยไม่ซ้ำกัน ถ้าสลากถูกสุ่มขึ้นมา 1 ใบ ความน่าจะเป็นที่จะได้สลากหมายเลขที่หารด้วย 2 หรือ 5 ลงตัว เท่ากับเท่าใด (ข้อสอบอัตนัย)
เฉลย
จำนวนสลากที่หารด้วย 2 หรือ 5 ลงตัว = จำนวนสลากที่หารด้วย 2 ลงตัว + จำนวนสลากที่หารด้วย 5 ลงตัว - จำนวนสลากที่หารด้วย 2 และ 5 ลงตัว
Note: จำนวนสลากที่หารด้วย 2 ลงตัว = (2, 4, 6, ... , 24) = 12
จำนวนสลากที่หารด้วย 5 ลงตัว = (5, 10, 15, 20, 25) = 5
จำนวนสลากที่หารด้วย 2 และ 5 ลงตัว = (10, 20) = 2
= 12 + 5 - 2
=15 ใบ
ดังนั้น ความน่าจะเป็นที่จะได้สลากหมายเลขที่หารด้วย 2 หรือ 5 ลงตัว = ¹⁵⁄₂₅ = 0.6
ตอบ 0.6
----------------------------------------------------------------------------------
6. วันทามีธนบัตรหนึ่งพันบาท 3 ฉบับ และธนบัตรห้าร้อยบาท 2 ฉบับ ถ้าวันทาสุ่มหยิบธนบัตรขึ้นมา 2 ฉบับพร้อมกัน แล้วความน่าจะเป็นที่ธนบัตร 2 ฉบับนี้ จะมีมูลค่ารวมกันมากกว่า 1,200 บาท เท่ากับเท่าใด (ข้อสอบอัตนัย)
เฉลย
มีธนบัตร 1,000 3 ฉบับ
มีธนบัตร 500 2 ฉบับ
จำนวนวิธีที่ได้สองใบมากกว่า 1,200 = จำนวนวิธีทั้งหมด - จำนวนวิธีที่ได้ธนบัตร 500 2 ฉบับ

ความน่าจะเป็นที่ธนบัตร 2 ฉบับนี้ จะมีมูลค่ารวมกันมากกว่า 1,200 บาท =

ตอบ 0.9
7. กล่องใบหนึ่งบรรจุสลาก 5 ใบที่มีหมายเลข 1, 3, 5, 7, 9 ใบละหนึ่งหมายเลข ถ้าสุ่มหยิบสลากในกล่องนี้ขึ้นมาสองใบ โดยหยิบทีละใบแบบไม่ใส่คืน แล้วนำหมายเลขที่ได้มาประกอบกันเป็นจำนวนสองหลัก โดยหมายเลขบนสลากใบแรกเป็นเลขโดดในหลักสิบ และหมายเลขบนสลากใบที่สองเป็นเลขโดดในหลักหน่วย ความน่าจะเป็นที่จะได้จำนวนสองหลักที่น้อยกว่า 60 เท่ากับข้อใด- ³⁄₁₀
- ⅖
- ½
- ⅗
- ¾
เฉลย
จำนวนวิธีทั้งหมด = 5 × 4 = 20 วิธี
จำนวนวิธีที่ได้จำนวนน้อยกว่า 60 = ใบแรกได้เลข 1, 3, 5 ใบที่สองเป็นเลขอะไรก็ได้ = 3 × 4 = 12 วิธี
Note: 3 มาจาก (1, 3, 5) 4 มาจากที่เหลือ 4 ใบ
ความน่าจะเป็นที่จะได้จำนวนสองหลักที่น้อยกว่า 60 = ¹²⁄₂₀ = ⅗
ตอบ ข้อ 4.
----------------------------------------------------------------------------------
นอกจากข้อสอบ O-NET เรื่องความน่าจะเป็นแล้ว เรายังมีข้อสอบคณิตศาสตร์เรื่องอื่น ๆ รวมไปถึงวิชาต่าง ๆ ที่นอกเหนือจากเลขอีกเพียบเลย คลิกดาวน์โหลดแอป StartDee แล้วไปสนุกกับควิซท้ายบทกันได้ที่แบนเนอร์ด้านล่างเลย
ส่วนตอนนี้เราแนะนำให้อ่านบทความเรื่อง การหาระยะทางระหว่างจุดสองจุด และ จุดกึ่งกลางของส่วนของเส้นตรง ไปก่อนได้เลยนะ






